
Therefore, I would like to ask the following questions.
Lattice energy equation ke free#
K at equilibrium Calculating Gibbs Free Energy 3 equations to use: Gibb. In 1918 Max Born and Alfred Landé proposed that the lattice energy could be derived from the electrostatic potential of the ionic lattice and a repulsive potential energy term. where b Repulsion coefficient or proportionality constant or Born coefficient. Read Online Free Energy Pogil Answers Key calculate the free energy change. The BornLandé equation is a means of calculating the lattice energy of a crystalline ionic compound. Moreover, I suspect it is the primary reason for the discrepancy between its calculated lattice energies and that of which are determined through the Born-Haber cycle. Theoretical calculation of lattice energy. However, the difference in electronegativity between the cation and the anion results in covalent characteristics which I believe can be further explained through Fajans' rule. The atoms of a crystal, which are arranged in a regular lattice. This Born-Lande equation is that equation that helps to determine the crystalline lattice. On the other hand, lattice energy is often used to describe the overall potential energy of ionic compounds. It is a measure of the cohesive forces that bind ionic solids. Lattice energy, as we say, is the energy generated when two different charged ions called cation and anion are mixed for forming an ionic solid. Thus +2 or -2 ions will release more lattice energy than the +1 or -1 ions. Lattice energy increases with increase of charge on the ions because of their more attractive force between them. The bonds between the cation and anion are assumed not to possess any covalent character. The kinetic energy of the emitted electrons depends on the frequency of the radiation. In chemistry, the lattice energy is the energy change upon formation of one mole of a crystalline ionic compound from its constituent ions, which are assumed to initially be in the gaseous state. Thus the attraction between them decreases and finally the less lattice energy released during the process.Madelung Constant - The Madelung constant is used in determining the electrostatic potential of a single ion in a crystal by approximating the ions by point charges. The corresponding Born exponent, $n$, and Madelung constant, $M$, must be determined empirically or theoretically for each ionic compound. Lattice Energy - (Measured in Joule per Mole) - The Lattice Energy of a crystalline solid is a measure of the energy released when ions are combined to make a compound.However, the most apparent limitations of the Born-Lande' equation I'm able to think of are as follows. born-landeequation solidstates latticeenergy in this video i have explained the derivation for the most important equation of solid states i.e born lande. of ions per formula unit Z(+), Z(-) charge on the cation and.
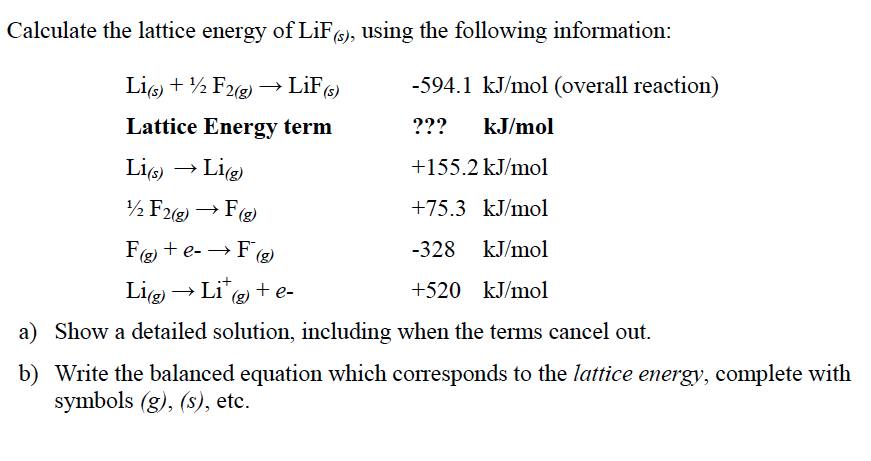
In which, $n$ is the Born exponent, $k_A$ is Avogradro's constant, $M$ is the Madelung constant, $e$ is the elementary charge, $\epsilon_\circ$ is the permittivity of free space, $z_1$ is the magnitude of the relative charge of the anion and $z_2$ is the magnitude of the relative charge of the cation with $r_\circ$ being their closest distance apart. Applying Kapustinskii equation U(L) 120250 ((vz(+)z(-) )/(d)) (1 - (34.5)/(d)) Where v No.
Lattice energy equation ke full#
Replacing r 0 as before yields the full Kapustinskii equation.The Born-Lande' equation is used to theoretically calculate the lattice energy, $\Delta U$, of ionic compounds. A cation (a positive ion) forms when a neutral atom loses one or more electrons from its valence shell, and an anion (a negative ion) forms when a neutral atom gains one or more electrons in its valence shell. The derivation of the later form of the Kapustinskii equation followed similar logic, starting from the quantum chemical treatment in which the final term is 1 − d / r 0 where d is as defined above. Finally, Kapustinskii noted that the Madelung constant, M, was approximately 0.88 times the number of ions in the empirical formula. In addition, the Born exponent, n, was assumed to have a mean value of 9.

Kapustinskii replaced r 0, the measured distance between ions, with the sum of the corresponding ionic radii.
U L = K ⋅ ν ⋅ | z + | ⋅ | z − | r + + r − ⋅ ( 1 − d r + + r − ) Lattice energy ( H l a t t ) is the energy required to separate 1 mol of an ionic compound into gaseous ions. Chapter 17: Ionic equilibria quiz Chapter 18: Lattice energy quiz Chapter 19: Moles and equations quiz Chapter 20: Nitrogen and sulfur quiz Chapter 21. The next level of sophistication is to link the eddy viscosity to the actual turbulent kinetic-energy density (unit-mass density for simplicity): k 12. It is named after Anatoli Fedorovich Kapustinskii who published the formula in 1956. The Kapustinskii equation calculates the lattice energy U L for an ionic crystal, which is experimentally difficult to determine.


 0 kommentar(er)
0 kommentar(er)
